meface/docs/article/gis/base/gcs&pgs.md

title	date	author	tags	categories
地图坐标系统	2020-10-24	ac	GIS基础知识	GIS

地图坐标系统

1. 简介

坐标系统是描述现实世界中物体存在的空间位置（坐标）的参照系，通过定义特定基准及其参数形式来实现。

由于地球的自然表面不是平整的，需要想办法用数学公式描述地球表面，只能设想一个近似的数学面。所以，下面进行三个逼近后用参考椭球表示地球的形状和大小。

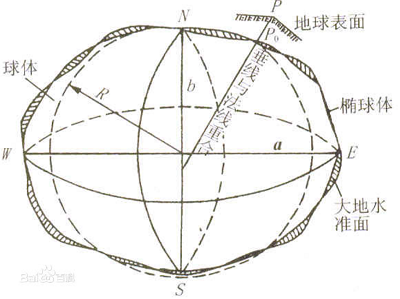
• 大地水准面是地球表面的第一级逼近。假设当海水处于完全静止的平衡状态时，从海平面延伸到所有大陆下部，而与地球重力方向处处正交的一个连续、闭合的曲面，这就是大地水准面。
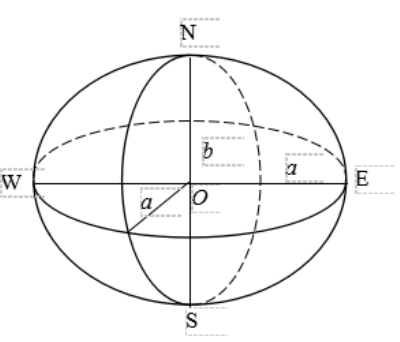
• 地球椭球体是地球表面的第二级逼近。大地水准面可以近似成一个规则成椭球体，但并不是完全规则，其形状接近一个扁率极小的椭圆绕短轴旋转所形成的规则椭球体，这个椭球体称为地球椭球体。
• 参考椭球体是地球表面的第三级逼近。是一个数学上定义的地球表面，它近似于大地水准面。 以参考椭球体的长半轴、短半轴和扁率来表示地球的形状和大小。

地球椭球体又称“地球椭圆体”和“地球扁球体”，代表地球大小和形状的数学曲面，以长半径a和扁率ɑ表示。因它十分迫近于椭球体，故通常以参考椭球体表示地球椭球体的形状和大小。椭圆绕其短轴旋转所成的形体，并近似于地球大地水准面。

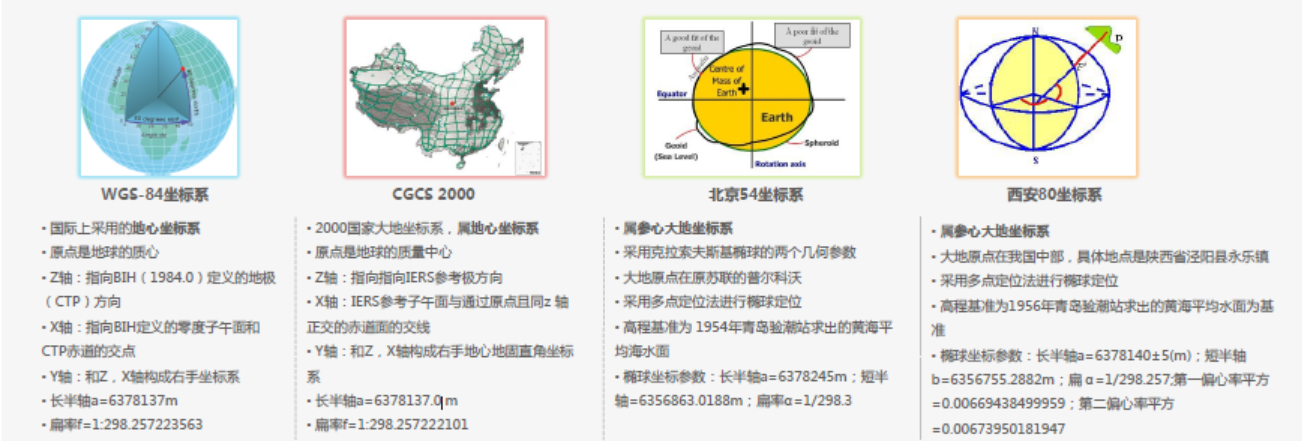
根据参考椭球的中心与地球质心的关系分为：

• 地心大地坐标系：指地球椭球的中心与地球质心重合。如CGCS2000、WGS84。
  

• 参心大地坐标系：指地球椭球的中心不与地球质心重合而是接近地球质心。
  

2.地理坐标系（GCS）

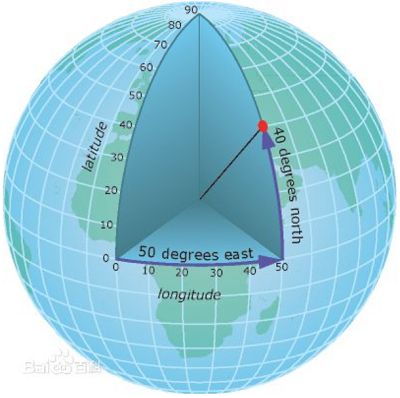
通过经纬度对地球表面点位置信息进行描述的坐标系，一个地理坐标系包括角度测量单位、本初子午线和参考椭球体三部分。所以地理坐标系依据其所选用的本初子午线、参考椭球的不同而略有区别。

经度和纬度是从地心到地球表面上某点的测量角。

GCS中经度和纬度值以十进制度为单位或以度、分和秒 (DMS) 为单位进行测量。

3.投影坐标系（PCS）

投影坐标系是基于地理坐标系，运用某种投影方式进行投影，将球面上的点位信息投影到平面上的坐标系。将球面坐标转化为平面坐标的过程称为投影。但地图投影永远不能绝对准确地表示球形地球。作为地图投影过程的结果，每张地图都会显示角度一致性，距离和面积的变形。

投影坐标系的实质是平面坐标系统，地图单位通常为米。

按变形性质分类：

• 等角投影：角度变形为零（Mercator）

• 等积投影：面积变形为零（Albers）

• 任意投影：长度、角度和面积都存在变形

其中，各种变形相互联系相互影响：等积与等角互斥，等积投影角度变形大，等角投影面积变形大。

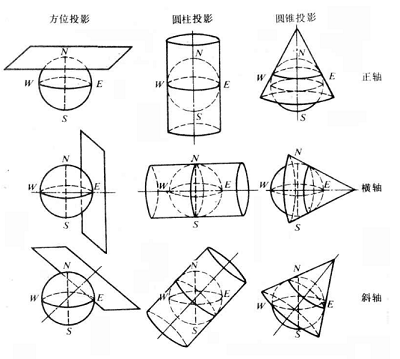
从投影面类型划分：

• 横圆柱投影：投影面为横圆柱

• 圆锥投影：投影面为圆锥

• 方位投影：投影面为平面

从投影面与地球位置关系划分为：

• 正轴投影：投影面中心轴与地轴相互重合
• 斜轴投影：投影面中心轴与地轴斜向相交
• 横轴投影：投影面中心轴与地轴相互垂直
• 相切投影：投影面与椭球体相切
• 相割投影：投影面与椭球体相割

4.常见的投影坐标系

下面介绍几种常见的投影：

4.1 高斯-克吕格投影

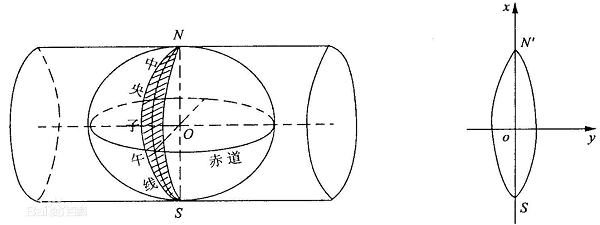
高斯-克吕格投影，又名"等角横切椭圆柱投影”，是地球椭球面和平面间正形投影的一种。

假想有一个椭圆柱与地球椭球体上某一经线相切，其椭圆柱的中心轴与赤道平面重合，将地球椭球体面有条件地投影到椭球圆柱面上高斯克吕格投影条件：

1. 中央经线和赤道投影为互相垂直的直线，且为投影的对称轴；
2. 具有等角投影的性质；
3. 中央经线投影后保持长度不变；

特点：

1. 中央子午线无变形
2. 无角度变形，图形保持相似
3. 离中央子午线越远，变形越大

高斯-克吕格投影在长度和面积上变形很小，中央经线无变形，自中央经线向投影带边缘，变形逐渐增加，变形最大之处在投影带内赤道的两端。由于其投影精度高，变形小，而且计算简便（各投影带坐标一致，只要算出一个带的数据，其他各带都能应用），因此在大比例尺地形图中应用，可以满足军事上各种需要，能在图上进行精确的量测计算。

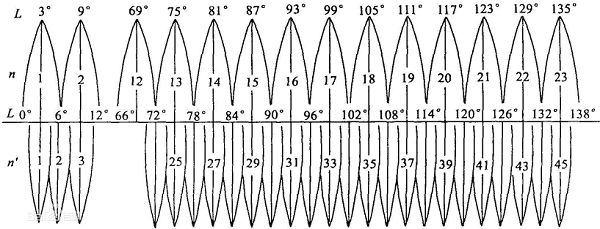
分带投影，通常按6度和3度进行分带投影。自0子午线起每隔经差3度或6度自西向东分带。

我国大中比例尺地图均采用高斯-克吕格投影：

• 1:2.5万~1:50万比例尺地形图采用6度。

• 1:10000 比例尺采用3度分带。

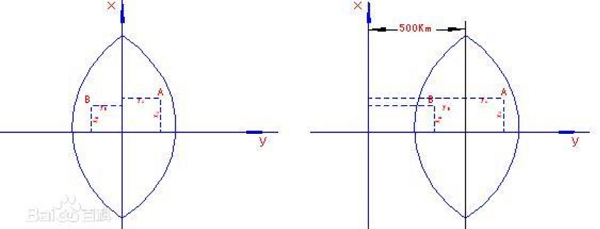
高斯平面直角坐标系

在投影面上，中央子午线和赤道的投影都是直线，以中央子午线和赤道的交点为原点，以中央子午线的投影为纵坐标X轴，以赤道的投影为横坐标Y轴。在我国x坐标都是正的，y坐标的最大值（在赤道上，6°带）约为330km。为了避免出现负的横坐标，可在横坐标上加上500 000m。此外还应在坐标前面再冠以带号。这种坐标称为国家统一坐标。

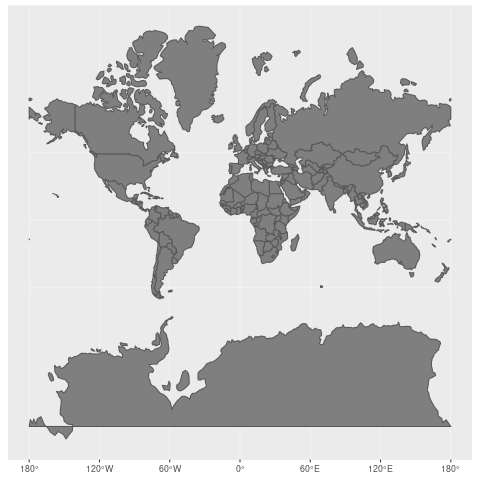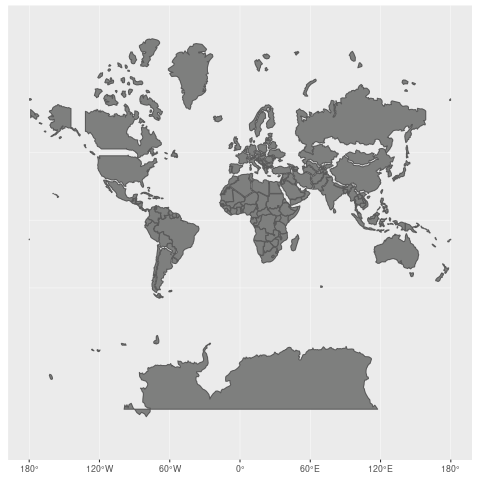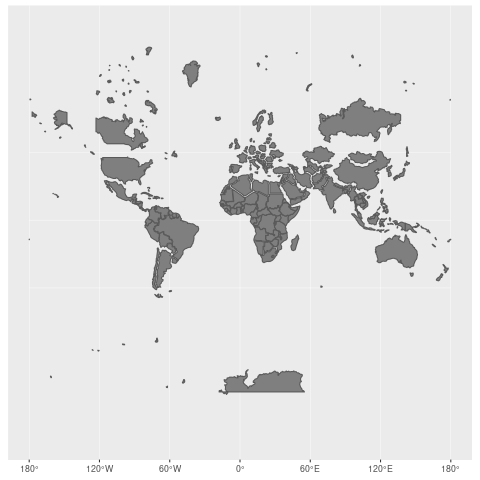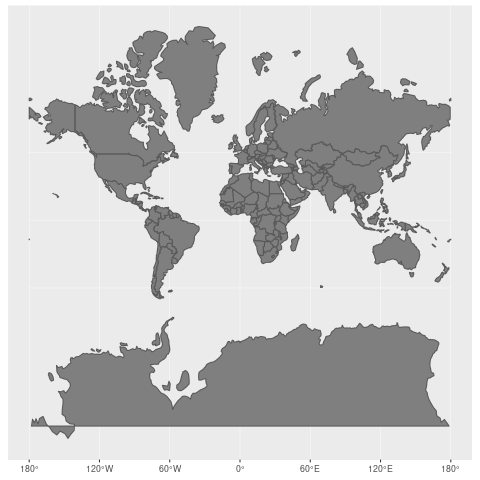
4.2 墨卡托投影

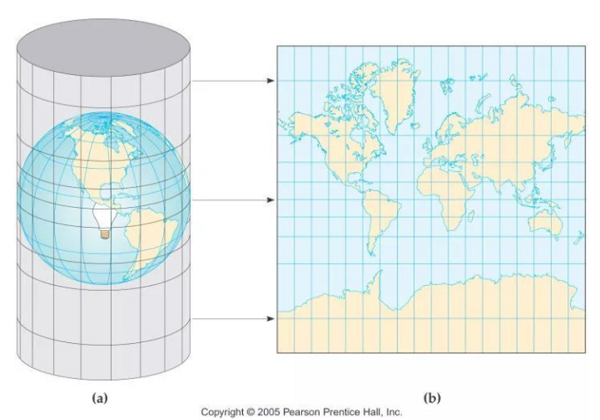
墨卡托投影又称“正轴等角切圆柱投影”，由荷兰地图学家墨卡托(G.Mercator)于1569年创拟。假设地球被套在一个圆柱中，赤道与圆柱相切，然后在地球中心放一盏灯，把球面上的图形投影到圆柱体上，再把圆柱体展开，就形成以一幅墨卡托投影的世界地图。

特点：

1. 没有角度变形，由每一点向各方向的长度比相等，
2. 经纬线都是平行直线，且相交成直角，经线间隔相等，纬线间隔从基准纬线处向两极逐渐增大。
3. 地图上长度和面积变形明显，但基准纬线处无变形，从基准纬线（赤道）处向两极变形逐渐增大， 但因为它具有各个方向均等扩大的特性，保持了方向和相互位置关系的正确（优点）。

4.3Web 墨卡托投影（基于WGS84）

Web Mercator 坐标系使用的投影方法不是严格意义的墨卡托投影，而是一个被 EPSG（European Petroleum Survey Group）称为伪墨卡托的投影方法，这个伪墨卡托投影方法的大名是 Popular Visualization Pseudo Mercator，PVPM。因为这个坐标系统是 Google Map 最先使用的，或者更确切地说，是Google 最先发明的。

在投影过程中，将表示地球的参考椭球体近似的作为正球体处理（正球体半径 R = 椭球体半长轴 a）。

由于基准面被篡改后，本来是等角投影的Mercator坐标变换算法，不再等角了，而是近似等角，也就是出现角度变形。

Web Mercator的wkid:

ESRI:102113 Esri 内部使用ID，与 EPSG:3785 相应。已被弃用。

ESRI:102100 Esri 内部使用ID，与 EPSG:3857 相应。

4.4UTM投影（通用墨卡尔投影）

UTM投影，属于等角横轴割圆柱投影，是墨卡托投影的推广。因投影圆柱与地球相割，中央经线投影后的长度比为0.9996，投影带各部分的长度变形比较平稳，其6°带内长度变形小于0.1%。

UTM 投影（Universal Transverse Mercator，通用横轴墨卡托投影）是由美国军方在1947提出的，美国本土采用Clarke 1866椭球体以外，UTM在世界其他地方都采用WGS 1984。因此起始分带并不在本初子午线，而是在180度，因而所有美国本土都处于0－30带内。

UTM投影采用6度分带，从东经180度（或西经180度）开始，自西向东算起，因此1带的中央经线为-177（-180 ~ -6），而0度经线为30带和31带的分界，这两带的分界分别是-3和3度。纬度采用8度分带，从80S到84N共20个纬度带（X带多4度），分别用C到X的字母来表示。为了避免和数字混淆，I和O没有采用。UTM的“false easting”值为500km，而南半球UTM带的“false northing”为10000km.。

“WGS 1984”坐标系的墨卡托投影分度带（UTM ZONE）选择方法如下：

• 北半球地区，选择最后字母为“N”的带；
• 根据经度计算带号，带号=（经度整数位/6）的整数部分+31， 如：江西省南昌新建县某调查单元经度范围115°35′20″~115°36′00″，带数=115/6+31=50，选50N，即WGS 1984 UTM ZONE 50 N
• 根据UTM投影带号计算最大经线或最小经线，如WGS_1984_UTM_Zone_49N，这个49的计算方法：从180度经度向东,每6度为一投影带,第49个投影带 ， 49=(114+180)/6，这个114为49投影带的最大经线。

5.国内常用的坐标系